La integral de trayectoria de Richard Feynman es tanto una poderosa máquina de predicción como una filosofía sobre cómo es el mundo. Pero los físicos todavía están luchando por descubrir cómo usarlo y qué significa
Por: Charlie Madera
(Quanta)-La fórmula más poderosa de la física comienza con una S delgada, el símbolo de una especie de suma conocida como integral. Más adelante viene una segunda S, que representa una cantidad conocida como acción. Juntas, estas S gemelas forman la esencia de una ecuación que podría decirse que es el adivino del futuro más efectivo que se haya ideado hasta ahora.
La fórmula oracular se conoce como integral de trayectoria de Feynman. Por lo que saben los físicos, predice con precisión el comportamiento de cualquier sistema cuántico: un electrón, un rayo de luz o incluso un agujero negro. La integral de trayectoria ha acumulado tantos éxitos que muchos físicos creen que es una ventana directa al corazón de la realidad.
“Así es realmente el mundo”, dijo Renate Loll, física teórica de la Universidad de Radboud en los Países Bajos.
Pero la ecuación, aunque adorna las páginas de miles de publicaciones de física, es más una filosofía que una receta rigurosa. Sugiere que nuestra realidad es una especie de mezcla, una suma, de todas las posibilidades imaginables. Pero no les dice a los investigadores exactamente cómo llevar a cabo la suma. Así que los físicos han pasado décadas desarrollando un arsenal de esquemas de aproximación para construir y calcular la integral para diferentes sistemas cuánticos.
Las aproximaciones funcionan lo suficientemente bien como para que físicos intrépidos como Loll busquen ahora la integral de trayectoria definitiva: una que combina todas las formas concebibles de espacio y tiempo y produce un universo con la forma del nuestro como resultado neto. Pero en esta búsqueda por demostrar que la realidad es de hecho la suma de todas las realidades posibles, se enfrentan a una profunda confusión sobre qué posibilidades deberían entrar en la suma.
Todos los caminos conducen a uno
La mecánica cuántica realmente despegó en 1926 cuando Erwin Schrödinger ideó una ecuación que describía cómo los estados ondulatorios de las partículas evolucionan de un momento a otro. La siguiente década, Paul Dirac avanzó una visión alternativa del mundo cuántico. La suya se basaba en la venerable noción de que las cosas toman el camino de “menor acción” para ir de A a B, la ruta que, en términos generales, requiere menos tiempo y energía. Richard Feynman luego tropezó con el trabajo de Dirac y desarrolló la idea, revelando la integral de ruta en 1948.
El corazón de la filosofía está a la vista en la demostración por excelencia de la mecánica cuántica: el experimento de la doble rendija.
Los físicos disparan partículas a una barrera con dos rendijas y observan dónde caen las partículas en una pared detrás de la barrera. Si las partículas fueran balas, formarían un grupo detrás de cada ranura. En cambio, las partículas caen a lo largo de la pared trasera en franjas repetidas. El experimento sugiere que lo que se mueve a través de las rendijas es en realidad una onda que representa las posibles ubicaciones de la partícula. Los dos frentes de onda emergentes se interfieren entre sí, produciendo una serie de picos donde la partícula podría acabar siendo detectada.
El patrón de interferencia es un resultado sumamente extraño porque implica que ambos caminos posibles de la partícula a través de la barrera tienen una realidad física.
La integral de trayectoria asume que así es como se comportan las partículas incluso cuando no hay barreras o rendijas alrededor. Primero, imagina cortar una tercera hendidura en la barrera. El patrón de interferencia en la pared del fondo cambiará para reflejar la nueva ruta posible. Ahora sigue cortando rendijas hasta que la barrera no sea más que rendijas. Por último, rellene el resto del espacio con «barreras» totalmente rendijas. Una partícula disparada a este espacio toma, en cierto sentido, todas las rutas a través de todas las rendijas hacia la pared del fondo, incluso rutas extrañas con desvíos en bucle. Y de alguna manera, cuando se resumen correctamente, todas esas opciones se suman a lo que esperaría si no hubiera barreras: un solo punto brillante en la pared del fondo.
Es una visión radical del comportamiento cuántico que muchos físicos toman en serio. “Lo considero completamente real”, dijo Richard MacKenzie, físico de la Universidad de Montreal.
Pero, ¿cómo puede un número infinito de trayectorias curvas sumarse a una sola línea recta? El esquema de Feynman, en términos generales, es tomar cada camino, calcular su acción (el tiempo y la energía necesarios para recorrer el camino) y, a partir de ahí, obtener un número llamado amplitud, que indica la probabilidad de que una partícula recorra ese camino. Luego sumas todas las amplitudes para obtener la amplitud total de una partícula que va de aquí para allá: una integral de todas las rutas.
Ingenuamente, los caminos desviados parecen tan probables como los rectos, porque la amplitud de cualquier camino individual tiene el mismo tamaño. De manera crucial, sin embargo, las amplitudes son números complejos. Mientras que los números reales marcan puntos en una línea, los números complejos actúan como flechas. Las flechas apuntan en diferentes direcciones para diferentes caminos. Y dos flechas que se alejan una de la otra suman cero.
El resultado es que, para una partícula que viaja por el espacio, las amplitudes de trayectorias más o menos rectas apuntan esencialmente en la misma dirección, amplificándose entre sí. Pero las amplitudes de los caminos sinuosos apuntan en todas direcciones, por lo que estos caminos trabajan uno contra el otro. Solo queda el camino en línea recta, lo que demuestra cómo el único camino clásico de acción mínima emerge de opciones cuánticas interminables.
Feynman demostró que su integral de trayectoria es equivalente a la ecuación de Schrödinger. El beneficio del método de Feynman es una receta más intuitiva sobre cómo lidiar con el mundo cuántico: sume todas las posibilidades.
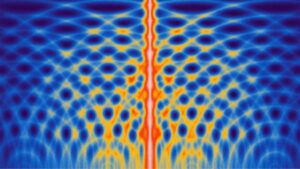
Suma de todas las ondas
Los físicos pronto llegaron a entender las partículas como excitaciones en campos cuánticos, entidades que llenan el espacio con valores en cada punto. Donde una partícula puede moverse de un lugar a otro a lo largo de diferentes caminos, un campo puede ondularse aquí y allá de diferentes maneras.
Afortunadamente, la integral de trayectoria también funciona para campos cuánticos. “Es obvio qué hacer”, dijo Gerald Dunne, físico de partículas de la Universidad de Connecticut. “En lugar de sumar todas las rutas, sumas todas las configuraciones de tus campos”. Usted identifica los arreglos iniciales y finales del campo, luego considera todos los antecedentes posibles que los vinculan.
El mismo Feynman se apoyó en la integral de trayectoria para desarrollar una teoría cuántica del campo electromagnético en 1949. Otros averiguarían cómo calcular acciones y amplitudes para campos que representan otras fuerzas y partículas. Cuando los físicos modernos predicen el resultado de una colisión en el Gran Colisionador de Hadrones en Europa, la integral de trayectoria es la base de muchos de sus cálculos. La tienda de regalos incluso vende una taza de café que muestra una ecuación que se puede usar para calcular el ingrediente clave de la integral de trayectoria: la acción de los campos cuánticos conocidos.
“Es absolutamente fundamental para la física cuántica”, dijo Dunne.
A pesar de su triunfo en física, la integral de trayectoria inquieta a los matemáticos. Incluso una simple partícula que se mueve por el espacio tiene infinitas rutas posibles. Los campos son peores, con valores que pueden cambiar de infinitas maneras en infinitos lugares. Los físicos tienen técnicas inteligentes para hacer frente a la torre tambaleante de infinitos, pero los matemáticos argumentan que la integral nunca fue diseñada para operar en un entorno tan infinito.
“Es como magia negra”, dijo Yen Chin Ong, físico teórico de la Universidad de Yangzhou en China que tiene experiencia en matemáticas. “Los matemáticos no se sienten cómodos trabajando con cosas en las que no está claro lo que está pasando”.
Sin embargo, obtiene resultados que están fuera de toda duda. Los físicos incluso han logrado estimar la integral de trayectoria de la fuerza fuerte, la interacción extraordinariamente compleja que mantiene unidas a las partículas en los núcleos atómicos. Usaron dos trucos principales para hacer esto. Primero, hicieron del tiempo un número imaginario, un extraño truco que convierte las amplitudes en números reales. Luego aproximaron el continuo espacio-tiempo infinito como una cuadrícula finita. Los practicantes de este enfoque de la teoría del campo cuántico «enrejado» pueden usar la integral de trayectoria para calcular las propiedades de los protones y otras partículas que sienten la fuerza fuerte, superando las matemáticas desvencijadas para obtener respuestas sólidas que coincidan con los experimentos.
«Para alguien como yo en física de partículas», dijo Dunne, «esa es la prueba de que funciona».
Espacio-Tiempo = ¿La Suma de Qué?
Sin embargo, el mayor misterio de la física fundamental se encuentra más allá del alcance experimental. Los físicos desean comprender el origen cuántico de la fuerza de gravedad. En 1915, Albert Einstein reformuló la gravedad como resultado de las curvas en el tejido del espacio y el tiempo. Su teoría reveló que la longitud de una vara de medir y el tictac de un reloj cambian de un lugar a otro; en otras palabras, que el espacio-tiempo es un campo maleable. Otros campos tienen una naturaleza cuántica, por lo que la mayoría de los físicos esperan que el espacio-tiempo también, y que la integral de trayectoria capture ese comportamiento.
La filosofía de Feynman es clara: los físicos deberían sumar todas las formas posibles del espacio-tiempo. Pero cuando consideramos la forma del espacio y el tiempo, ¿exactamente qué es posible?
Es posible que el espacio-tiempo se divida, por ejemplo, separando un lugar de otro. O podría perforarse con tubos (agujeros de gusano) que unen las ubicaciones. Las ecuaciones de Einstein permiten formas tan exóticas, pero prohíben los cambios que conducirían a ellas; las rasgaduras o fusiones violarían la causalidad y generarían paradojas de viajes en el tiempo. Sin embargo, nadie sabe si el espacio-tiempo y la gravedad podrían involucrarse en una actividad más atrevida a nivel cuántico, por lo que los físicos no saben si arrojar o no espacio-tiempos de queso suizo a la «integral de la trayectoria gravitatoria».
Un campo sospecha que todo entra. Stephen Hawking, por ejemplo, defendió una integral de ruta que se adapta a rasgaduras, agujeros de gusano, donas y otros cambios «topológicos» salvajes entre las formas del espacio. Se apoyó en el truco de los números imaginarios por tiempo para hacer las matemáticas más fáciles. Hacer que el tiempo sea imaginario lo convierte efectivamente en otra dimensión del espacio. En una arena tan atemporal, no existe una noción de causalidad para que los universos desgarrados o plagados de agujeros de gusano se estropeen. Hawking usó esta integral de trayectoria «euclidiana» atemporal para argumentar que el tiempo comenzó en el Big Bang y para contar los bloques de construcción del espacio-tiempo dentro de un agujero negro. Recientemente, los investigadores utilizaron el enfoque euclidiano para argumentar que la información se escapa de los agujeros negros moribundos.
Este «parece ser el punto de vista más rico a tomar», dijo Simon Ross, un teórico de la gravedad cuántica de la Universidad de Durham. «La integral del camino gravitacional, definida para incluir todas las topologías, tiene algunas propiedades hermosas que aún no entendemos completamente».
Pero la perspectiva más rica tiene un precio. A algunos físicos no les gusta eliminar un elemento de carga de la realidad como el tiempo. La integral de la ruta euclidiana «realmente no es física», dijo Loll.
Su campo se esfuerza por mantener el tiempo en el camino integral, situándolo en el espacio-tiempo que conocemos y amamos, donde las causas preceden estrictamente a los efectos. Después de pasar años desarrollando formas de aproximarse a esta integral de trayectoria mucho más formidable, Loll ha encontrado indicios de que el enfoque puede funcionar. En un artículo, por ejemplo, ella y sus colaboradores sumaron un montón de formas estándar de espacio-tiempo (que se aproximaban a cada una como una colcha de pequeños triángulos) y obtuvieron algo parecido a nuestro universo: el espacio-tiempo equivalente a mostrar que las partículas se mueven en líneas rectas.
Otros están avanzando en la integral del camino atemporal para el espacio-tiempo y la gravedad, con todos los cambios topológicos incluidos. En 2019, los investigadores definieron rigurosamente la integral completa, no solo una aproximación, para universos bidimensionales, sino que utilizaron herramientas matemáticas que enturbiaron aún más su significado físico. Tal trabajo solo profundiza la impresión, tanto entre los físicos como entre los matemáticos, de que la integral de trayectoria tiene un poder que espera ser aprovechado.
«Tal vez todavía tenemos que definir bien las integrales de ruta», dijo Ong, «pero fundamentalmente creo que es solo cuestión de tiempo».



