La criptografía de celosía promete proteger los secretos de los ataques de las computadoras cuánticas del futuro lejano
Leila Sloman-Quanta Magazine
En 1994, el científico informático Peter Shor descubrió que si alguna vez se inventaran las computadoras cuánticas, diezmarían gran parte de la infraestructura utilizada para proteger la información compartida en línea. Esa aterradora posibilidad ha hecho que los investigadores se apresuren a producir nuevos esquemas de encriptación «poscuánticos», para evitar que la mayor cantidad de información posible caiga en manos de piratas informáticos cuánticos.
A principios de este año, el Instituto Nacional de Estándares y Tecnología reveló cuatro finalistas en su búsqueda de un estándar de criptografía poscuántica. Tres de ellos usan «criptografía de celosía», un esquema inspirado en celosías, arreglos regulares de puntos en el espacio.
La criptografía de celosía y otras posibilidades poscuánticas difieren de los estándares actuales en formas cruciales. Pero todos se basan en la asimetría matemática. La seguridad de muchos sistemas criptográficos actuales se basa en la multiplicación y la factorización: cualquier computadora puede multiplicar rápidamente dos números, pero podría llevar siglos factorizar un número criptográficamente grande en sus constituyentes principales. Esa asimetría hace que los secretos sean fáciles de codificar pero difíciles de decodificar.
Lo que Shor reveló en su algoritmo de 1994 fue que una peculiaridad de la factorización lo hace vulnerable al ataque de las computadoras cuánticas. “Es algo muy específico y especial que puede hacer la computadora cuántica”, dijo Katherine Stange , matemática de la Universidad de Colorado, Boulder. Entonces, después de Shor, los criptógrafos tenían un nuevo trabajo: encontrar un conjunto novedoso de operaciones matemáticas que fueran fáciles de hacer pero casi imposibles de deshacer.
La criptografía de celosía es uno de los intentos más exitosos hasta ahora. Originalmente desarrollado en la década de 1990, se basa en la dificultad de realizar ingeniería inversa en las sumas de puntos.
Esta es una forma de describir la criptografía de celosía: imagine que su amigo tiene una celosía, que es solo un montón de puntos en un patrón regular que se repite en todo el plano. Tu amigo quiere que nombres 10 de estos puntos. Pero está siendo difícil y no dibujará todo el entramado. En cambio, enumera solo dos puntos: el primero con un valor de x de 101 y un valor de y de 19, el otro con coordenadas [235, 44].
Afortunadamente, es fácil encontrar nuevos puntos en un enrejado, porque cuando sumas y restas dos puntos en un enrejado, obtienes un tercer punto en el mismo enrejado. Así que todo lo que tienes que hacer es sumar los puntos que te dio tu amigo, o multiplicarlos por números enteros y luego sumarlos, o alguna combinación de los dos. Haz esto de ocho maneras diferentes y podrás responder la pregunta de tu amigo.
Pero tu amigo todavía no está satisfecho. Te da los mismos dos puntos de partida y luego te pregunta si puedes encontrar un punto cerca de [0, 0] en la misma red. Para responder correctamente a esta pregunta, debe encontrar la combinación de [101, 19] y [235, 44] que lo acerque a [0, 0]. Este problema es mucho más difícil que el primero, y probablemente termines adivinando y verificando para obtener la respuesta. Esa asimetría es lo que subyace a la criptografía de celosía.
Si realmente desea utilizar la criptografía de celosía para compartir información, debe hacer lo siguiente. Imagina que un amigo (¡más simpático!) quiere enviarte un mensaje seguro. Empiezas con una cuadrícula cuadrada de números. Digamos que tiene dos filas y dos columnas, y se ve así:

Ahora se le ocurre una «clave» privada que solo usted conoce. En este ejemplo, digamos que su clave privada son solo dos números secretos: 3 y −2. Multiplicas los números de la primera columna por 3 y los de la segunda columna por −2. Sume los resultados de cada fila para obtener una tercera columna con dos entradas.

Pegue la nueva columna al final de su cuadrícula. Esta nueva cuadrícula de tres columnas es su clave pública. ¡Compártelo libremente!
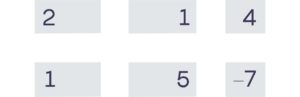
(Un escenario del mundo real será un poco más complicado. Para evitar que los piratas informáticos decodifiquen su clave privada, debe agregar un poco de ruido aleatorio en su columna final. Pero aquí vamos a ignorar ese paso por simplicidad. )
Ahora tu amigo usará la clave pública para enviarte un mensaje. Piensa en dos números secretos propios: 2 y 0. Multiplica los números de la primera fila por 2 y los de la segunda fila por 0. Luego suma los resultados de cada columna para obtener una tercera fila.

Ahora adjunta la nueva fila a la parte inferior de la cuadrícula y se la devuelve. (Nuevamente, en un sistema real, necesitaría agregar algo de ruido a su fila).
Ahora leerás el mensaje. Para hacer esto, verifique si la última fila de su amigo es correcta. Aplique su propia clave privada a las dos primeras entradas de su fila. El resultado debe coincidir con la última entrada.

Tu amigo también puede optar por enviarte una fila con un número incorrecto en la última columna. Ella sabe que este número no coincidirá con sus cálculos.

Si tu amigo envía una fila donde el último número es correcto, lo interpretarás como un 0. Si envía una fila donde el número es incorrecto, lo interpretarás como un 1. Por lo tanto, la fila codifica un solo bit: 0 o 1.
Tenga en cuenta que un atacante externo no tendrá acceso ni a su clave privada ni a la de su amigo. Sin ellos, el atacante no tendrá idea si el número final es correcto o no.
En la práctica, le gustaría enviar mensajes de más de un bit de longitud. Entonces, las personas que quieran recibir, digamos, un mensaje de 100 bits generarán 100 columnas nuevas en lugar de solo una. Luego, el remitente del mensaje creará una sola fila nueva, modificando las últimas 100 entradas para codificar un 0 o un 1 para cada entrada.
Si realmente se implementa la criptografía de celosía, tendrá innumerables matices que no se contemplan en este escenario. Por ejemplo, si desea que el mensaje esté realmente a salvo de miradas indiscretas, la matriz debe tener una cantidad impensable de entradas, lo que hace que todo sea tan difícil de manejar que no vale la pena usarlo. Para evitar esto, los investigadores usan matrices con simetrías útiles que pueden reducir la cantidad de parámetros. Más allá de eso, hay un conjunto completo de ajustes que se pueden aplicar al problema en sí, a la forma en que se incorporan los errores y más.
Por supuesto, siempre es posible que alguien encuentre una falla fatal en la criptografía de celosía, tal como lo hizo Shor con la factorización. No hay garantía de que un esquema criptográfico en particular funcione frente a cualquier posible ataque. La criptografía funciona hasta que se descifra. De hecho, a principios de este verano , se descifró un prometedor esquema de criptografía poscuántica utilizando no una computadora cuántica, sino una computadora portátil ordinaria. Para Stange, todo el proyecto crea una paradoja incómoda: «Lo que me parece tan sorprendente de la criptografía es que hemos construido esta infraestructura para la raza humana con la firme creencia de que nuestra capacidad como humanos es limitada», dijo. “Es tan atrasado”.



