Tres estudiantes de secundaria y su mentor revisaron un teorema centenario para demostrar que todos los nudos se pueden encontrar en un fractal llamado esponja de Menger
Por Gregorio Barber-Quanta Magazine
En otoño de 2021, Malors Espinosa se propuso idear un tipo especial de problema matemático. Como sucede con cualquier buena pregunta de investigación, tendría que ser estimulante y su solución no trivial, algo que otros quisieran estudiar. Pero una restricción adicional lo dejó perplejo. Malors, entonces estudiante de posgrado en matemáticas en la Universidad de Toronto, quería que los estudiantes de secundaria pudieran demostrarlo.
Durante años, Malors había organizado talleres de verano para estudiantes de secundaria locales, enseñándoles las ideas básicas de la investigación matemática y mostrándoles cómo escribir demostraciones. Pero algunos de sus estudiantes parecían dispuestos a hacer más: descubrir qué significa hacer matemáticas cuando no hay una clave de respuestas. Solo necesitaban la pregunta correcta para guiarlos.
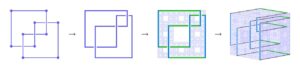
Malors finalmente encontró uno mientras leía un libro de texto sobre el caos. En sus páginas, se encontró con un objeto familiar: un fractal, o forma autosimilar, llamada esponja de Menger, que tiene una construcción simple pero elegante. Primero divide un cubo en lo que parece un cubo de Rubik. Quita el cubo del centro, junto con el cubo central de cada una de las seis caras. Luego repite este proceso para cada uno de los 20 cubos restantes. Y repite. Y repite. Verás rápidamente por qué el fractal resultante se llama esponja: con cada iteración, sus poros se multiplican exponencialmente.
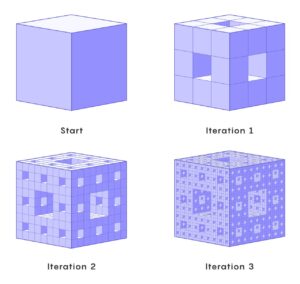
Desde que Karl Menger presentó su esponja fractal hace casi un siglo, ha cautivado la imaginación de matemáticos tanto profesionales como aficionados. Una de las razones: se ve genial. En 2014, cientos de entusiastas de las matemáticas participaron en un esfuerzo global, llamado MegaMenger, para construir versiones finitas de 200 libras de la esponja a partir de tarjetas de presentación. Debido a su estructura porosa, similar a la espuma, la esponja también se ha utilizado para modelar amortiguadores y formas exóticas del espacio-tiempo.
Pero lo más importante es que el fractal posee varias propiedades matemáticas contraintuitivas. Si se siguen extrayendo trozos cada vez más pequeños, lo que comenzó como un cubo se convierte en algo completamente distinto. Después de infinitas iteraciones, el volumen de la forma se reduce a cero, mientras que su superficie se vuelve infinitamente grande. Tal es la rareza de los fractales: flotando en algún lugar entre dimensiones, ocupando el espacio sin llenarlo realmente.

Cuando definió por primera vez su esponja en 1926, Menger también demostró que cualquier curva concebible (líneas y círculos simples, estructuras que parecen árboles o copos de nieve, polvos fractales) se puede deformar y luego incrustar en algún lugar de la esponja. Se puede hacer que se desplacen a lo largo de los contornos intrincados de la esponja sin abandonar nunca su superficie, sin golpear un agujero o sin cruzarse consigo mismas. La esponja, escribió Menger, era, por lo tanto, una “curva universal”.
Pero, como Malors se dio cuenta más tarde, esto planteaba una nueva pregunta. Menger había demostrado que se podía encontrar un círculo en su esponja. Pero ¿qué sucede con los objetos que, en cierto sentido, eran equivalentes al círculo? Consideremos un nudo matemático: una cuerda que se ha retorcido y atado, cuyos extremos se han cerrado para formar un bucle. Desde fuera, podría parecer un lío enredado, pero una hormiga que caminara a lo largo de él acabaría volviendo al punto de partida, tal como sucedería en un círculo. De este modo, todo nudo es equivalente, u “homeomorfo”, a un círculo.

La afirmación de Menger no distinguía entre curvas homeomorfas. Su prueba sólo garantizaba, por ejemplo, que el círculo podía encontrarse en su esponja, no que todos los nudos homeomorfos pudieran encontrarse, con sus bucles y enredos todavía intactos. Malors quería demostrar que se podían encontrar todos los nudos dentro de la esponja.
Parecía la combinación perfecta para entusiasmar a los jóvenes matemáticos, que recientemente se habían divertido aprendiendo sobre nudos en su seminario. ¿Y a quién no le gustan los fractales? La pregunta era si el problema sería abordable. “Realmente esperaba que hubiera una respuesta”, dijo Malors.
Así fue. Después de unos pocos meses de reuniones semanales por Zoom con Malors, tres de sus estudiantes de secundaria —Joshua Broden, Noah Nazareth y Niko Voth— pudieron demostrar que todos los nudos se pueden encontrar dentro de la esponja de Menger.(abre una nueva pestaña)Además, descubrieron que probablemente se puede decir lo mismo de otro fractal relacionado.
«Es una forma inteligente de combinar las cosas», dijo Radmila Sazdanovic ,(abre una nueva pestaña)Una topóloga de la Universidad Estatal de Carolina del Norte que no participó en el trabajo añadió que, al revisar el teorema de Menger, que tiene un siglo de antigüedad, Malors —que suele investigar en el campo tan dispar de la teoría de números— aparentemente había planteado una pregunta que nadie había pensado antes en plantear. “Es una idea muy, muy original”, dijo.
Una forma diferente de ver los nudos
Broden, Nazareth y Voth habían asistido a varios talleres de verano de Malors a lo largo de los años. Cuando les enseñó por primera vez sobre nudos en un taller anterior, «me quedé atónito cuando tenía 14 años», dijo Voth.
Pero el problema de Menger sería la primera vez que iban más allá de los cuadernos de ejercicios escolares con hojas de respuestas. “Fue un poco estresante, porque era la primera vez que hacía algo para lo que realmente nadie tenía la respuesta, ni siquiera Malors”, dijo Nazareth. Tal vez no había ninguna respuesta.
Su objetivo era básicamente enhebrar una aguja de coser microscópica en una nube de polvo (el material que quedaba de la esponja después de muchas extracciones). Tendrían que introducir el alfiler en los lugares adecuados, atar los nudos con una precisión inmaculada y no soltar nunca la esponja. Si el hilo acababa flotando en los agujeros vacíos de la esponja para hacer algún nudo, se acababa el juego.
No es una tarea fácil, pero había una manera de simplificarla. Los nudos se pueden representar en una hoja de papel plana como diagramas especiales llamados presentaciones de arco. Para crear uno, se comienza con información sobre cómo las hebras del nudo pasan una por delante o por detrás de la otra. Luego se aplica un conjunto de reglas para traducir esta información en una serie de puntos en una cuadrícula. Cada fila y columna de la cuadrícula contendrá exactamente dos puntos.
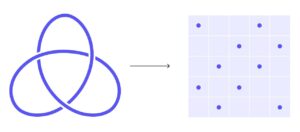
Conecta estos puntos con líneas horizontales y verticales. Cada vez que dos segmentos se crucen, dibuja el segmento vertical delante del segmento horizontal.
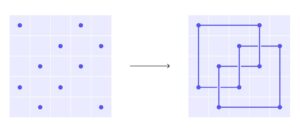
Todos los nudos se pueden representar de esta manera, similar a una cuadrícula. Aunque la representación en forma de arco puede parecer a veces más complicada que otras formas de dibujar el nudo, facilita a los matemáticos el estudio de algunas de las propiedades más importantes del nudo.
Cuando los estudiantes observaron los diagramas de líneas entrecruzadas, recordaron las caras de la esponja de Menger. Sería bastante sencillo colocar las líneas horizontales de una presentación en arco en una cara de la esponja y las líneas verticales en la cara opuesta. La dificultad estaría en averiguar cómo conectar el nudo, cómo estirarlo de nuevo hasta las tres dimensiones. En cada una de las esquinas de la presentación en arco, las dos caras tendrían que estar conectadas a través del interior de la esponja sin golpear accidentalmente un agujero.
Para asegurarse de que esto siempre fuera posible, los matemáticos recurrieron a lo que se conoce como el conjunto de Cantor, un análogo unidimensional de la esponja de Menger. Para construir el conjunto, se parte de un segmento de línea y se lo divide en tercios. Se quita el tercio del medio, se hace lo mismo con los dos segmentos restantes, y así sucesivamente hasta el infinito. Quedará una dispersión de puntos.
El equipo analizó tanto una esponja de Menger como un conjunto de Cantor que habían sufrido el mismo número de pasos de eliminación. Se dieron cuenta de que en los puntos de las caras de la esponja cuyas coordenadas están ambas en el conjunto de Cantor no debería haber ningún agujero. Es más, tampoco debería haber agujeros en ningún lugar directamente detrás de esos puntos, gracias al diseño repetitivo de la esponja. Por lo tanto, un nudo quedaría libre y sin obstáculos para pasar sin saltar accidentalmente del material de la esponja.
Todo lo que quedaba, entonces, era que los estudiantes demostraran que siempre podían comprimir o estirar la presentación del arco de un nudo dado de modo que todos sus vértices se alinearan con las coordenadas del conjunto de Cantor. (Se permitía esa compresión y estiramiento porque no afectaría la estructura general de la presentación del arco y, por lo tanto, el nudo que representa).
Para completar este paso final, Broden, Nazareth y Voth tomaron un atajo. Demostraron que podían deformar cualquier presentación de arco de modo que los puntos donde se cruzaban sus segmentos verticales y horizontales estuvieran en el conjunto de Cantor. Esto garantizaba automáticamente que el mayor número de vértices también se alinearía con el conjunto de Cantor. En otras palabras, siempre podían incrustar un nudo determinado en alguna iteración de la esponja de Menger.
Ahora que habían respondido a la pregunta original de Malors, querían llevar su resultado más allá. Ya habían comenzado a investigar si todos los nudos también podrían estar incrustados en una versión tetraédrica de la esponja de Menger:

“Fue sorprendentemente molesto”, dijo Broden. Sin la comodidad de tener caras alineadas directamente una frente a la otra, su método para empujar nudos a través del fractal ya no funcionaría.
Medido en nudos
Según Malors, fue en esta etapa cuando los estudiantes aprendieron el dolor de la investigación matemática: que gran parte de la disciplina implica luchar contra el fracaso de una vía de ataque prometedora. “Nos enfrentamos a las matemáticas, y las matemáticas no tienen piedad”, dijo. “Con las matemáticas tal como se presentan a los estudiantes de secundaria, generalmente están protegidos de eso”.
Malors, por su parte, estaba convencido de que no se podía encontrar un nudo de trébol en el tetraedro. Durante una llamada de Zoom, los tres estudiantes se resistieron. Abandonaron la reunión, recordaron, sintiéndose desanimados y frustrados. Pero decidieron seguir con sus instintos. Un par de semanas después, para sorpresa de Malors, regresaron con un resultado: habían descubierto una nueva forma de representar la presentación en arco del nudo de trébol en el tetraedro. Más tarde demostraron que esto se podía hacer para todos los nudos «pretzel», la clase más general de nudos a la que pertenece el trébol, aunque la cuestión sigue abierta para otros tipos de nudos.
Malors conjetura que los métodos de los estudiantes podrían ofrecer una manera de medir la complejidad de los fractales de manera más amplia. No todos los fractales tienen la garantía de admitir todo tipo de nudos. Tal vez su estructura pueda entenderse mejor en función de qué tipos de nudos pueden y no pueden admitir.
Como mínimo, la obra podría inspirar arte nuevo, similar al concurso MegaMenger de 2014. “Sería maravilloso ver esto construido con materiales físicos”, dijo Allison Moore.(abre una nueva pestaña), un teórico de nudos de la Universidad Commonwealth de Virginia.
Mientras tanto, Broden, Nazareth y Voth ya se han graduado de la escuela secundaria. Sólo Broden ha decidido seguir trabajando en el problema del tetraedro (cuando no está ocupado con los cursos universitarios), pero los tres están considerando carreras en matemáticas. «Me parece significativo que esté tratando de contribuir a algo más grande que yo, a la naturaleza de la verdad», dijo Nazareth. Todo comienza con hacer la pregunta correcta.



