Investigadores de la Universidad de Oxford proponen COIN, un método novedoso de compresión de imágenes que almacena los pesos de un MLP sobreajustado a una imagen y supera a JPEG a velocidades de bits bajas incluso sin codificación de entropía.
(synced)-En un nuevo artículo, los investigadores de la Universidad de Oxford presentan un enfoque novedoso de compresión de imágenes que supera al estándar JPEG a velocidades de bits bajas, incluso sin codificación de entropía o sin aprender una distribución sobre pesos.
Los métodos de codificación automática desarrollados recientemente para la compresión de imágenes con pérdida han atraído la atención de las comunidades de procesamiento de imágenes y aprendizaje automático. Dichos codificadores automáticos funcionan según un principio simple: una imagen, típicamente modelada como un vector de intensidades de píxeles, se cuantifica, reduciendo así la cantidad de información necesaria para almacenarla o transmitirla.
En lugar de almacenar los valores RGB para cada píxel de una imagen, el enfoque propuesto almacena los pesos de una red neuronal sobreajustada a la imagen. Los investigadores llaman a su método ‘COIN’ (Representaciones neurales implícitas empeñadas).
COIN codifica una imagen superponiéndola con un pequeño perceptrón multicapa (MLP), un tipo de red neuronal artificial de retroalimentación. El enfoque asigna las ubicaciones de los píxeles a los valores RGB (a menudo denominados representación neuronal implícita) y luego transmite los pesos de este MLP. En el momento de la decodificación, el MLP transmitido se evalúa en todas las ubicaciones de los píxeles para reconstruir la imagen.
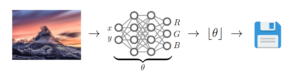
La parte más difícil de todo el proceso de compresión de imágenes es el sobreajuste de los MLP, debido a la información de alta frecuencia dentro de las imágenes naturales. Los enfoques recientes han empleado codificaciones y activaciones sinusoidales para mitigar este proceso, y el nuevo estudio descubre que el uso de MLP con activaciones sinusoidales puede ajustar imágenes grandes (393k píxeles) con redes sorprendentemente pequeñas (8k parámetros).
Para reducir el tamaño del modelo, los investigadores aplican la búsqueda de arquitectura y la cuantificación del peso. Realizan un barrido de hiperparámetros sobre el ancho y el número de capas MLP, cuantificando los pesos de precisión de 32 bits a 16 bits, que es suficiente para superar el estándar JPEG para velocidades de bits bajas.
El otro aspecto destacado de COIN es la flexibilidad adicional de su enfoque de decodificación. Las imágenes se pueden decodificar progresivamente simplemente evaluando funciones en varias ubicaciones de píxeles. La decodificación parcial de imágenes de esta manera es difícil para los métodos anteriores basados en codificadores automáticos.
Para probar el rendimiento de COIN, los investigadores realizaron experimentos en el conjunto de datos de imágenes de Kodak que comprende 24 imágenes de tamaño 768 × 512. El modelo se comparó con tres modelos de compresión neuronal basados en autocodificadores (BMS, MBT y CST). También compararon COIN con los códecs de imagen JPEG, JPEG2000, BPG y VTM.
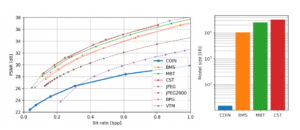
Los investigadores identificaron primero combinaciones válidas de profundidad y ancho para los MLP que representan una imagen (por ejemplo, para 0.3 bpp usando pesos de 16 bits) para determinar las mejores arquitecturas de modelo para un presupuesto de parámetro dado (medido como bits por píxel o bpp). Los resultados muestran que a bajas tasas de bits, el modelo propuesto mejora el estándar JPEG incluso sin el uso de codificación de entropía.

Los experimentos demuestran que COIN supera al estándar JPEG después de 15k iteraciones y luego continúa mejorando constantemente; y esa calidad de compresión depende de la elección de la arquitectura, con diferentes arquitecturas óptimas para diferentes valores de bpp. El equipo de Oxford dice que espera que el trabajo adicional en esta área conduzca a una nueva clase de métodos para la compresión de datos neuronales.
El documento COIN: Compresión con representaciones neuronales implícitas está en arXiv .
Autor : Hecate He



