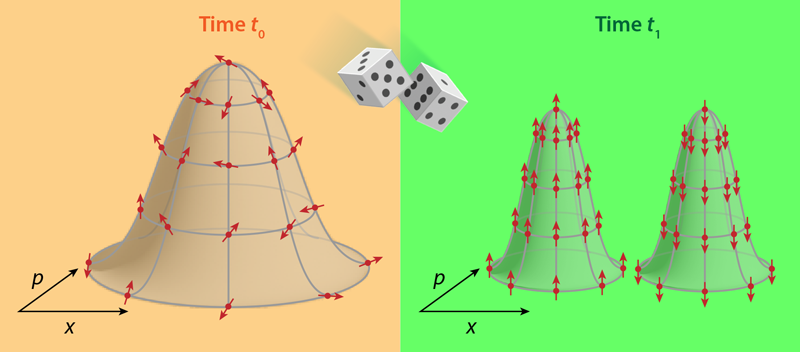
Un modelo propuesto une la teoría cuántica con la gravedad clásica al suponer que los estados evolucionan de forma probabilística, como un juego de azar
Por: Thomas Galera-Instituto de Óptica Cuántica e Información Cuántica, Viena, Austria
(Physics)-La mejor teoría de la materia de los físicos es la mecánica cuántica, que describe el comportamiento discreto (cuantizado) de partículas microscópicas mediante ecuaciones de ondas. Su mejor teoría de la gravedad es la relatividad general, que describe el movimiento continuo (clásico) de cuerpos masivos a través de la curvatura espacio-temporal. Estas dos teorías de gran éxito parecen estar fundamentalmente en desacuerdo sobre la naturaleza del espacio-tiempo: las ecuaciones de ondas cuánticas se definen en un espacio-tiempo fijo, pero la relatividad general dice que el espacio-tiempo es dinámico y se curva en respuesta a la distribución de la materia. La mayoría de los intentos de resolver esta tensión se han centrado en la cuantificación de la gravedad, siendo las dos propuestas principales la teoría de cuerdas y la gravedad cuántica de bucles. Pero un nuevo trabajo teórico de Jonathan Oppenheim del University College de Londres propone una alternativa: dejar la gravedad como teoría clásica y acoplarla a la teoría cuántica mediante un mecanismo probabilístico [ 1 ]. Esta estrategia híbrida se consideraba tradicionalmente imposible, ya que se pensaba que daba lugar a inconsistencias [ 2 ]. Oppenheim evita estos escollos, pero a costa de tener que insertar probabilidad –una “tirada de dados”– en la evolución del espacio-tiempo. Experimentos futuros podrían probar la viabilidad de este enfoque probando si la gravedad es cuántica.
Durante los últimos 70 años uno de los problemas más importantes de la física fundamental ha sido reconciliar la física cuántica con la relatividad general. Hay dos estrategias para esta unificación: cuantificar la gravedad o encontrar una manera de insertar materia cuántica en un marco gravitacional clásico. La primera es claramente la preferida, pero ninguna de las propuestas de gravedad cuántica ha sido confirmada experimentalmente todavía. Eso parecería dejar una oportunidad para la otra estrategia, pero los teóricos han demostrado (a través de los llamados teoremas de no-go) que acoplar la materia cuántica a la gravedad clásica conduce a inconsistencias, como violaciones del famoso principio de incertidumbre de Heisenberg. De hecho, el modelo más conocido de este acoplamiento cuántico-clásico, la ecuación semiclásica de Einstein [ 3 ], adolece de las inconsistencias predichas por estos teoremas de no-go.
Con su nuevo enfoque, Oppenheim evita las barreras de los teoremas de no-go al abandonar uno de sus supuestos subyacentes: que el acoplamiento entre la gravedad clásica y la materia cuántica es reversible [ 4 ]. En una teoría reversible, el estado del sistema en cualquier momento dado se puede utilizar, junto con las ecuaciones de movimiento, para determinar de forma única el estado del sistema en cualquier otro momento del pasado o del futuro. Sin embargo, no todas las teorías tienen por qué ser reversibles, también pueden ser estocásticas. En una teoría estocástica, el estado inicial de un sistema físico evoluciona según una ecuación, pero sólo se puede saber probabilísticamente qué estados podrían ocurrir en el futuro; no existe un estado único que se pueda predecir.
Oppenheim desarrolla una teoría estocástica que se basa en dos enfoques estadísticos separados para las partes cuántica y clásica de un sistema. En la descripción estadística del lado cuántico, los estados se describen utilizando operadores de densidad que evolucionan como si el sistema fuera abierto, es decir, susceptible a influencias incontroladas del entorno. En la descripción estadística del lado clásico, los estados son distribuciones de probabilidad en el espacio de fases, un marco que a menudo se utiliza para modelar grandes cantidades de partículas, donde no se conoce la posición individual ni el momento de cada partícula.
Oppenheim une estas dos descripciones estadísticas en un estado cuántico clásico, que consiste en una distribución de probabilidad clásica en el espacio de fases, combinada con un operador de densidad cuántica que se define en cada punto de ese espacio de fases (Fig. 1 ). Por ejemplo, una partícula podría tener un 15% de probabilidad de estar en alguna región del espacio de fases, y su estado de espín en esa región podría ser una superposición igual de estados arriba y abajo.
El siguiente paso es derivar una ecuación general para el acoplamiento entre los sistemas clásico y cuántico del estado cuántico clásico. A diferencia de los acoplamientos anteriores (reversibles), el acoplamiento estocástico de Oppenheim no mezcla características cuánticas y clásicas: preserva la naturaleza de cada sistema. Por ejemplo, el acoplamiento garantiza que no se viole el principio de incertidumbre en el sistema cuántico ni que se produzcan señales más rápidas que la luz en el sistema clásico. La ecuación resultante tiene múltiples partes: una evolución hamiltoniana reversible tanto para el sistema clásico como para el cuántico, la decoherencia del sistema cuántico, así como «saltos» probabilísticos entre estados. Estos saltos pueden corresponder a una medición que divide la distribución de probabilidad de una partícula en dos partes, una correspondiente a cada resultado de la medición.
Habiendo determinado la forma general de los acoplamientos clásico-cuánticos, Oppenheim centra su atención en el acoplamiento de la teoría cuántica de campos (QFT) con la relatividad general. Específicamente, los campos cuánticos en el espacio-tiempo curvo se acoplan a la métrica clásica de la relatividad general mediante la ecuación de acoplamiento estocástico. La relatividad general impone entonces restricciones adicionales a la forma de esta ecuación general. Un primer requisito es que exista un límite clásico en el que se recuperen las ecuaciones de movimiento estándar de la relatividad general. La segunda es que las leyes de la física parecen iguales para todos los observadores. A partir de estos requisitos, Oppenheim obtiene una teoría híbrida que presenta una reacción inversa estocástica de los campos en el espacio-tiempo curvo; en otras palabras, los campos cuánticos pueden cambiar la curvatura del espacio-tiempo como se requeriría de una unificación de la relatividad general y QFT. Los enfoques existentes para QFT no tienen esta característica: tratan la curvatura como fija. Por tanto, el nuevo modelo tiene el potencial de describir una interacción fundamental entre QFT y la relatividad general.
La propuesta de Oppenheim es en cierto sentido muy radical: va en contra de 70 años de sabiduría aceptada por la comunidad de la física fundamental. Sin embargo, en otro sentido es muy conservador: preserva la naturaleza clásica de la relatividad general y, por lo tanto, evita claramente la multitud de dificultades conceptuales que enfrentan las propuestas de unificación existentes. Por ejemplo, el espacio-tiempo determina las relaciones causales entre eventos, y cualquier teoría que cuantice el espacio-tiempo enfrenta el problema de qué significa que la estructura causal tenga propiedades cuánticas, como las superposiciones de órdenes causales. Pero cambiar la cuantidad por la estocasticidad tiene sus propias dificultades conceptuales. Por ejemplo, Oppenheim descubre que la información cuántica puede perderse en un agujero negro, un resultado que muchos físicos podrían encontrar inaceptable. También existen cuestiones fundamentales sobre el origen de los saltos probabilísticos.
Entonces, ¿qué sigue para esta nueva teoría de la materia cuántica y la gravedad clásica? Como ocurre con todas las teorías físicas, la verdadera prueba radica en su concordancia con los datos experimentales. El modelo puede verse limitado por mediciones del tiempo de coherencia de un objeto masivo en una superposición cuántica, ya que el tiempo de coherencia puede relacionarse con la evolución de la métrica del espacio-tiempo. Los datos existentes de tiempo de coherencia ya se han utilizado para descartar ciertos rangos de parámetros para modelos híbridos cuánticos clásicos como el de Oppenheim [ 5 ]. Una prueba empírica aún más decisiva de estos modelos podría provenir de propuestas para determinar experimentalmente si el campo gravitacional es clásico [ 6 , 7 ] (ver Sinopsis: Una prueba del lado cuántico de la gravedad ). La idea es entrelazar dos objetos masivos sólo con su interacción gravitacional, lo que implicaría que la gravedad es cuántica en su base. Actualmente hay grupos experimentales trabajando intentando mejorar sus configuraciones para poder llevar a cabo estos experimentos. Ha comenzado la carrera para determinar si esta nueva propuesta prevalecerá sobre los enfoques establecidos.
Referencias
- J. Oppenheim, «¿Una teoría poscuántica de la gravedad clásica?» Física. Rev. X 13 , 041040 (2023) .
- CM DeWitt y D. Rickles, El papel de la gravitación en la física: Informe de la Conferencia de Chapel Hill de 1957 , vol. 5 (Instituto Max Planck de Historia de la Ciencia, Berlín, 2011).
- C. Møller, “El complejo energía-momento en la relatividad general”, Teorías relativistas de la gravitación , editado por A. Lichnerowicz y MA Tonnelat Colloq. En t. CNRS vol. 91 (1962).
- TD Galley et al. , “Cualquier acoplamiento consistente entre la gravedad clásica y la materia cuántica es fundamentalmente irreversible”, Quantum 7 , 1142 (2023) .
- J. Oppenheim et al. , “Decoherencia inducida gravitacionalmente versus difusión espacio-temporal: probando la naturaleza cuántica de la gravedad”, (2022) arXiv:2203.01982 .
- S. Bose y col. , “Testigo del entrelazamiento de espines para la gravedad cuántica”, Phys. Rev. Lett. 119 , 240401 (2017) .
- C. Marletto y V. Vedral, “El entrelazamiento inducido gravitacionalmente entre dos partículas masivas es evidencia suficiente de efectos cuánticos en la gravedad”, Phys. Rev. Lett. 119 , 240402 (2017) .