Una nueva demostración que involucra a cientos de átomos entrelazados pone a prueba la interpretación de Schrödinger del experimento mental clásico de Einstein, Rosen y Podolsky
Por: margaret d reid-Centro de Ciencia y Tecnología Cuántica, Universidad Tecnológica de Swinburne, Melbourne, Australia
(Physics)-En 1935, Einstein, Podolsky y Rosen (EPR) presentaron un argumento que, según ellos, implica que la mecánica cuántica proporciona una descripción incompleta de la realidad [ 1 ]. El argumento se basa en dos supuestos. Primero, si el valor de una propiedad física de un sistema se puede predecir con certeza, sin perturbar el sistema, entonces hay un «elemento de realidad» para esa propiedad, lo que significa que tiene un valor incluso si no se mide. En segundo lugar, los procesos físicos tienen efectos que actúan localmente en lugar de instantáneamente a distancia. Posteriormente, John Bell propuso una forma de probar experimentalmente estas suposiciones de «realismo local» [ 2 ], y las llamadas pruebas de Bell las han invalidado desde entonces para sistemas de unas pocas partículas pequeñas, como electrones o fotones [ 3]. Ahora Paolo Colciaghi y sus colegas de la Universidad de Basilea, Suiza, han probado el argumento de EPR para un sistema más grande que comprende nubes de cientos de átomos [ 4 ]. Sus resultados cuestionan la validez del realismo local de EPR para sistemas masivos mesoscópicos.
EPR consideró un sistema de dos partículas separadas espacialmente, A y B, que tienen pares de observables que no conmutan, como su posición y momento. Los sistemas están preparados para que las posiciones de las partículas estén correlacionadas y sus momentos estén anticorrelacionados. Esta relación entre observables significa que un experimentador debería ser capaz de determinar la posición o el momento de la partícula A con certeza al realizar la medición adecuada de B. Es importante destacar que el sistema está configurado para que las partículas estén «separadas como en el espacio», lo que significa no puede haber perturbación de A debido a una medición en B.
Asumiendo el realismo local, EPR concluyó que las posiciones y los momentos de las partículas están simultáneamente bien definidos. Pero la mecánica cuántica no permite valores simultáneos y definidos con precisión tanto para la posición como para el momento. EPR propuso resolver esta paradoja sugiriendo que la mecánica cuántica es incompleta, lo que implica que una teoría completa incluiría lo que los físicos ahora denominan variables ocultas locales, una posibilidad que las pruebas de Bell han descartado desde entonces [2 , 3 ] .
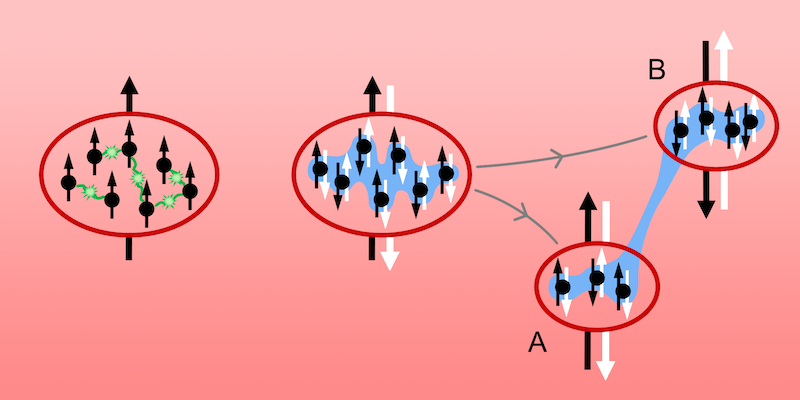
Mientras que la mayoría de las pruebas de Bell se han realizado en pares de partículas individuales, Colciaghi y sus colegas utilizan nubes de varios cientos de átomos de rubidio-87. Comienzan preparando un solo condensado de Bose-Einstein en una trampa y diseñan una interacción para enredar los átomos del condensado (Fig. 1). Una vez liberado de la trampa, el condensado se expande para formar dos nubes entrelazadas separadas por hasta 100 µm. Para probar la paradoja, es necesario medir dos observables que no conmutan. En lugar de usar la posición y el momento como prevé EPR, Colciaghi y sus colegas usan «pseudoespines», un par de estados cuánticos que, como el espín, constituyen un sistema de dos niveles. Estos «giros» están definidos por dos niveles hiperfinos, con el giro de cada nube determinado por la cantidad de átomos en un nivel menos la cantidad de átomos en el otro nivel. Para medir el primero de los observables de espín que no conmutan, los átomos en cada nivel se cuentan directamente. El segundo observable de espín complementario se mide mediante un pulso que interactúa con los átomos antes del conteo. Las pruebas de EPR que utilizan conjuntos atómicos se han realizado antes [ 5– 7 ], pero aquí hay una diferencia importante: en este experimento, la elección de la configuración de medición, es decir, cuál de los dos giros no conmutativos se mide, se realiza de forma independiente para cada nube. Esta independencia es esencial para una genuina paradoja EPR; sin ella no podemos descartar una influencia entre los sistemas [ 8 ].
Colciaghi y sus colegas prueban las correlaciones de EPR al determinar los errores al inferir el giro de la nube A a partir de las mediciones del giro de la nube B, primero cuando los pulsos están ausentes y luego nuevamente cuando los pulsos se aplican tanto para A como para B. Si bien no es cero , el producto de estos errores es pequeño en relación con el límite inferior del producto de incertidumbre de Heisenberg medido en el experimento. Por lo tanto, se confirma la paradoja, ya que los espines que no conmutan para A pueden inferirse con una precisión no cuantificable por ningún estado cuántico local para A [ 9 ]. Sin embargo, si estas correlaciones son el resultado de una medición realizada en B que de alguna manera afecta el resultado en A por medios no clásicos, entonces el experimento, que involucra una gran cantidad de átomos, es intrigantemente macroscópico.
Luego, los investigadores hacen una modificación muy reveladora a su experimento. En 1935, Schrödinger respondió al argumento de EPR con su famoso ejemplo del gato en estado de superposición [ 10]. Menos conocida es su propuesta de una situación en la que los parámetros de medición se ajustan de modo que dos variables complementarias se midan simultáneamente, “una por medición directa, la otra por medición indirecta”. Schrödinger se preguntó si los valores de ambas variables se determinarían con precisión para esta elección de configuración de medición (cuando la configuración es fija pero antes de que finalice la medición), y cuestionó si esta determinación de valores sería compatible con la mecánica cuántica. Colciaghi y sus colegas crean tal escenario manipulando los pulsos que determinan qué espín se mide: manteniendo fija la configuración de la nube B, cambian la configuración de la nube A.
Los investigadores muestran que pueden medir el valor de una variable de la nube A directamente, mientras infieren el valor de la variable complementaria indirectamente a partir de una medición en la nube B. Además, ajustando la configuración de A nuevamente, muestran cómo la correlación con la se recupera la medición en B. Esto ilustra que cambiar la configuración de la nube A no cambia la corrección de la predicción hecha para la variable complementaria en A al medir B. ¿Este hallazgo implica que hay un elemento de realidad para el resultado de la medición en A una vez que la configuración? en B es fijo? Para la medida directa de cada variable, el sistema está preparado para el conteo de átomos en los dos niveles después de cualquier interacción de los átomos con los pulsos, cuando se determinan los ajustes de medida. ¿Los átomos que serían contados ya están en esos niveles, se lleve a cabo o no el conteo? La naturaleza mesoscópica del experimento parecería reforzar el argumento de Schrödinger: parece que los valores de los observables se fijarían una vez que se determinen los parámetros de medición, pero antes de que finalicen las mediciones contando los átomos.
Las implicaciones de los resultados no están del todo claras. Para confirmar el valor obtenido indirectamente en A se requiere una interacción adicional para cambiar la configuración, lo que significa que el estado cuántico cambia. Por lo tanto, la proposición de que los valores de ambos giros se determinan antes de la medición no viola el principio de incertidumbre; ni son los valores excluidos por el teorema de Bell, que se refiere a las variables definidas antes de las interacciones que fijan la configuración. Sin embargo, como observó Schrödinger, parece que, según la mecánica cuántica, después de la medición indirecta en B, el sistema A se describe mediante una función de onda para la cual el valor medido indirectamente es, como dijo Schrödinger, «totalmente nítido», pero el valor medido directamente es “totalmente indeterminado” [ 10]. Schrödinger cuestionó además la legitimidad de los valores simultáneos para la posición x y para el momento p al demostrar que el valor de x 2 + p 2 , cuando los dos observables se miden simultáneamente, debe ser un número entero impar, a pesar de que x y p son continuos y por lo tanto, aparentemente no está sujeto a esta restricción [ 10 ]. Tales preguntas permanecen abiertas y bien pueden aclararse mediante un examen más detenido del experimento reciente.
Referencias
A.Einstein et al. , “¿Puede considerarse completa la descripción mecánico-cuántica de la realidad física?” física Rev. 47 , 777 (1935) .
JS Bell, «Sobre la paradoja de Einstein Podolsky Rosen», Physics 1 , 195 (1964) .
N.Brunner et al. , “No localidad de Bell”, Rev. Mod. física 86 , 419 (2014) .
-
Colciaghi et al. , «Experimento de Einstein-Podolsky-Rosen con dos condensados de Bose-Einstein», Phys. Rev. X 13 , 021031 (2023) .
-
Peise et al. , «Satisfacer el criterio de Einstein-Podolsky-Rosen con partículas masivas», Nat. común 6 , 8984 (2015) .
-
Fadel et al. , «Patrones de entrelazamiento espacial y dirección de Einstein-Podolsky-Rosen en condensados de Bose-Einstein», Science 360 , 409 (2018) .
-
Kunkel et al. , «El entrelazamiento multipartito distribuido espacialmente permite la dirección EPR de las nubes atómicas», Science 360 , 413 (2018) .
-
Aspect et al. , «Prueba experimental de las desigualdades de Bell utilizando analizadores variables en el tiempo», Phys. Rev. Lett. 49 , 1804 (1982) .
MD Reid et al. , “ Coloquio : La paradoja de Einstein-Podolsky-Rosen: De los conceptos a las aplicaciones”, Rev. Mod. física 81 , 1727 (2009) .
-
Schrödinger, “Die gegenwärtige Situation in der Quantenmechanik,” Naturwissenschaften 23 , 844 (1935) , [“La situación actual de la mecánica cuántica,” Sci. Nat. 23 , 844 (1935)].